圧縮（座屈）に付いて

一番憂鬱だった、圧縮（座屈）に付いて説明します。

これは、計算自体は大して面倒くさいものでは無いのですが、全てを説明するとなると積分なんかも出てくるのでどうしようかと考えておりましたが、ここはその部分を端折って公式とプログラムで省略することにしました。

フリープログラムはフカダソフト様 ≫フリーソフト ≫ 断面性能の計算 Ver.1.0

断面係数、断面2次モーメント等の公式一覧表はこちら

まずは、圧縮と座屈の違いから説明していきますが、また例によってかなり簡単に感覚的に説明しますので、神経質な方や正確無比を信条としている方は心臓に悪いので見ないほうが良いかと思います。

まず、イメージしていただくのは、変形の仮定が想像しやすいのでゴムのパイプなんかがいいでしょうか？

直径20ｃｍくらいで、パイプの厚さが3㎝位のものを2本、片方は長さが30㎝くらいでもう片方は2000mm位とします。

例えば地面において上からすこしづつ荷重をかけて行くとある程度の重量のところで、短い方のパイプ（短柱）は周囲が膨らんで樽のような形になってくると想像できるはずです。

ゴムなので荷重を減らしていくとと元の形状に戻りますが、これが金属だったらある程度の変形をしたらもう元に戻れなくなり、それを塑性変形というということはすでにお話しております。

では、2000mmの長い方のパイプ（長柱）に力をかけて行くとどうなるでしょう？

ゴムなのでポキッとは行きませんが、折れてしまいますよね？まぁ、これもかかっていた荷重を無くすると元のパイプに戻るとは思うんですが、普通の金属であれば戻りません。

このゴムが塑性変形を起こす方を圧縮とし、折れてしまう方を座屈とします。

塑性変形を起こすものは、圧縮で強度を算出すれば良いですし、座屈するものに関しては座屈で強度を検討すれば良いのですが、では中間の長さの場合はどうでしょうか？

中間の長さというのは、力をかけて行った時に、どうなるかの想像がつかない長さのことで、この場合だとどのくらいでしょうか？・・・60㎝くらい？もうちょっと長いですか？

長さはまぁ想像にお任せして、塑性変形すると言われればそんな感じもするし、座屈すると言われればそんな感じもするんだけど・・・といった場合です。

こんなゴムのパイプであれば実際にどうなるかの実験も出来ますが、ユーザー様に強度検討書の作成を依頼された、例えば世界に数台しかない超希少車両の部品に係る荷重が座屈なのか圧縮なのかを調べるために壊れるまで力をかけていくわけには行きません。

また、このへんの基準を曖昧にしておくと、強度検討などは都合のいいように作成されてしまいますので、明確な判断基準が設定されているんです。

それを判断するのが、細長比（「ほそながひ」とか「さいちょうひ」読みます）となり、λ（ラムダ）で表されます。

λ ＝ L/ｒ

L は柱の長さ・・・（本来は小文字なのですが、「1」や「I」と、見間違えやすいので大文字で記しています）

ｒは断面回転半径・・・ $r = \sqrt \frac{I}{A}$

I ＝断面二次モーメント　・・・公式もしくはプログラムで算出（端折りNo1)

A＝断面積

これによって算出された数値が、下表中の「細長比の範囲」内にあれば座屈で算出、範囲を超えていれば圧縮で算出します。

	鋳鉄	軟鋼	硬鋼	木材
σ_D(kg/mm²)	55.98	33.95	48.94	4.99
a	$\frac{1}{1600}$	$\frac{1}{7500}$	$\frac{1}{5000}$	$\frac{1}{750}$
細長比の範囲	$<80\sqrt{n}$	$<90\sqrt{n}$	$<85\sqrt{n}$	$<60\sqrt{n}$

細長比の算出において必要となる「ｎ」は端末係数で、柱の端末の形状によって異なります。（下図参照）

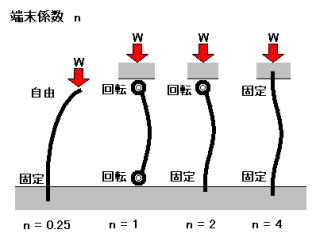
通常自動車の部品では、両端が回転端、片側固定片側固定（移動）端、両端固定端のいずれかが使用されると思います。

回転端はコントロールアームのブッシュ部分やピロボールのようなものを言い、固定端は溶接やボルト止により柱の固定部分が、回転や移動をしないように固定されているものを言います。

リーフスプリングに使われるシャックルは、両側が回転しますので両側回転端、端末係数ｎ＝１となります。

回転端は、回転のみに自由度を与えられており、移動端は移動する自由を与えられている状態を言い、固定端はそのいずれも制限されている状態を言います。

今回仮定したゴムの柱は、固定もしておりませんし、移動や回転も自由にできませんので該当する項目がありませんが、通常の構造物でただ置いてあるだけの状態というのは非常に不安定ですので存在しないとおもって頂いて構いません。

また、鋳物では無いことがわかってはいるけれども、使用されている鋼材が「軟鋼」なのか「硬鋼」なのかの区別がつかない場合、使用されている材質の炭素含有量を調べ、その炭素含有量が0.30％以下のものは「軟鋼」0.30を超えるものは「硬鋼」となります。

これは下記のJISハンドブック（左が一次製品版素材について、右が二次製品版、形鋼等です）などで調べる他、一般的によく使われる材料等であればネットなどで検索しても出てきます。

他にも「オイラー式」「テトマイヤー式」「ジョンソン式」などありますが、知りたい人はご自身の力でお調べください。では、細長比の算出の結果、細長比の範囲内であった場合、座屈の計算を行うこととなりますが、上記表の適用範囲は、「ランキン式」という座屈強度算出方法用の表ですので、ランキンの式を使用して算出いたします。

ランキン式による座屈応力 σ の算出

σ＝ $\displaystyle \frac{\sigma_{D}}{1+\frac{a\lambda^2}{C}}$

この時の　σ_D並びに　a　は、上表中の材料の圧縮強度の　σ_D並びに実験定数　a　を使用する。

応力 σ が算出されたら、続いてその柱が耐えうることの出来る座屈荷重 Pc の算出を行います。

Pc＝σ ・A　・・・A は柱の断面積となります。（断面が途中で変化している場合は、最小断面部の断面積を使用します）

ここまで算出されれば、安全率ｆを算出することが出来ます。

ｆ＝ $\displaystyle\frac{P_{c}}{P}$ 　≧ 1.6であること。

P はその柱にかかる荷重値となります。

今回の座屈に関しては、表内より鋼材の種類による圧縮強度を抜粋しておりますので、使用される材料による引張強度や降伏点からの算出はしません。

では細長比で適用範囲外となってしまった場合はどうするか・・・。

この場合は圧縮に係る強度を算出しますので、座屈よりも計算がはるかに簡単になります。

まずは、応力 σ を算出します。

σ＝ $\frac{F}{A}$

この時、 F は柱にかかる荷重、A は柱の断面積（断面が変化する場合は最面積が最小となる部分の面積）とする。

と、ここまでは、引張強度の算出と同じですが、ここからちょっとだけ変わります。

圧縮強度 σ_Dの算出

σ_D＝ σ_b× 0.9

σ_bは材料の引張強度

これは、せん断の場合のせん断強度と同様に、引張強度から圧縮強度算出しておりますので、降伏点については算出の必要がありません。

応力と強度が出ておりますので、もう安全率ｆを算出できます。

ｆ＝ $\displaystyle\frac{\sigma_{D}}{\sigma}$ 　≧ 1.6であること。

となり、基本的に引張強度の算出と変わりませんが、材料の引張強度に0.9 を乗じて圧縮強度とします。

なお、本文中で上からの荷重を主体として話を進めてまいりましたが、座屈や圧縮だけに限らず荷重の向きは上から下というものだけではありません。

上は線路が熱の影響で膨張し、逃げのクリアランスだけで収集がつかなくなった結果座屈したものです。

このように上下方向の向きだけでなく、また一方からの荷重だけという以外にも様々な荷重のかかり方がありますので、正確に荷重の方向やかかっている荷重がどのような力なのかを正確に見極めることが出来るようにしてください。

これで、憂鬱だった圧縮（座屈）の解説を終了させていただきます。

-　基本事項

-　圧縮（座屈）について　⇐　 Now